Workshop SAMOURAI


When & where

The workshop will take place IRL, on December 10-11, 2024 at Institut Henri Poincaré, Paris.
Room: amphithéâtre Hermite (ground floor).




Presentation of the workshop

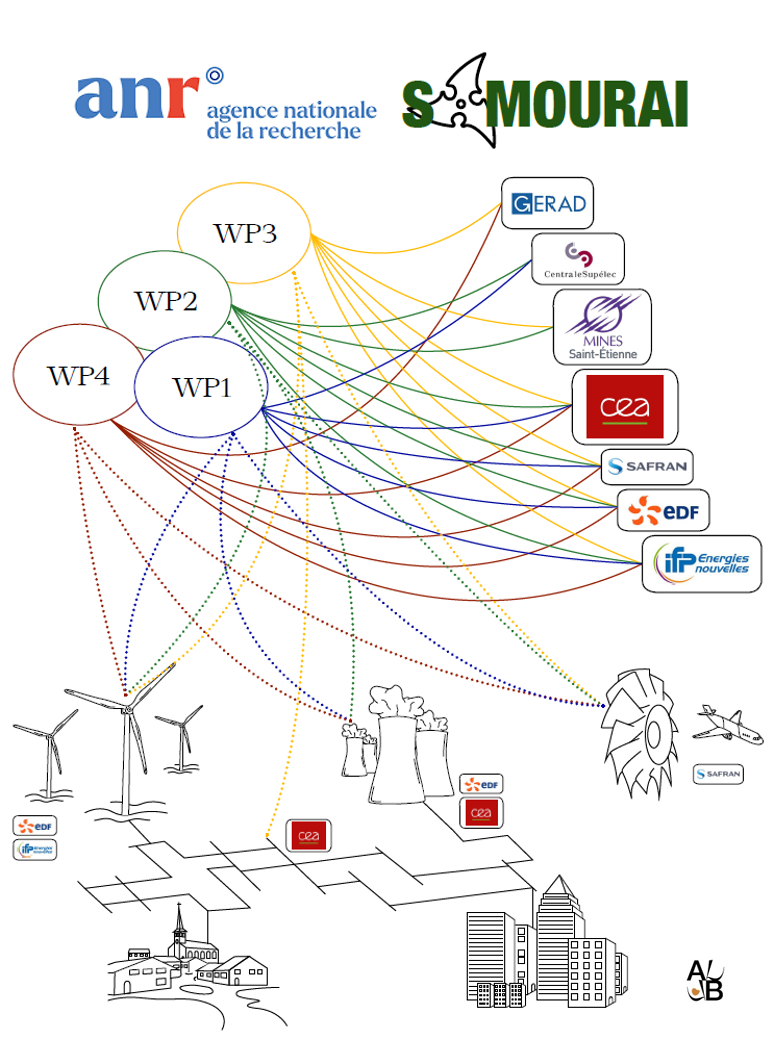
Workshop of the SAMOURAI ANR project (ANR-20-CE46-0013)
Simulation Analytics and Meta-model-based solutions for Optimization, Uncertainty and Reliability AnalysIs

Organizers: Delphine Sinoquet, Morgane Menz (IFPEN)

SAMOURAI TEAM
♣ CEA: Amandine Marrel (WP leader), Gabriel Sarazin
♣ CentraleSupélec: Romain Ait Abdelmalek-Lomenech, Julien Bect (WP leader), Emmanuel Vazquez
♣ EDF: Vincent Chabridon (WP leader), Bertrand Iooss, Merlin Keller (WP leader), Julien Pelamatti, Sanaa Zannan
♣ EMSE: Rodolphe Le Riche (CNRS LIMOS, WP leader), Babacar Sow
♣ IFPEN: Reda El Amri, Morgane Menz, Miguel Munoz Zuniga (WP leader), Delphine Sinoquet (Project leader)
♣ Polytechnique Montréal: Sébastien Le Digabel (WP leader), Christophe Tribes
♣ Safran: Raphaël Carpintero Perez (CMAP), Sébastien Da Veiga (ENSAI, formerly Safran) Brian Staber (WP leader)


Registration

Registration is free, but compulsory.


Agenda

December 10

December 11

Speakers

Invited researchers

Nathalie Bartoli (ONERA) abstract slides

Mickaël Binois (Centre Inria d'Université Côte d'Azur) abstract slides

François-Xavier Briol (University College London) abstract slides

Wenlin Chen (University of Cambridge) abstract slides

SAMOURAI speakers

Romain Ait Abdelmalek-Lomenech (L2S, CentraleSupélec) abstract slides

Raphaël Carpintero Perez (CMAP/ Safran) abstract

Vincent Chabridon (EDF) abstract slides

Sébastien Le Digabel (Polytechnique Montréal) & Merlin Keller (EDF) abstract slides

Rodolphe Le Riche (CNRS LIMOS) & Julien Pelamatti (EDF) abstract slides

Amandine Marrel (CEA) & Bertrand Iooss (EDF) abstract slides

Morgane Menz & Miguel Munoz Zuniga (IFPEN) abstract slides part1 slides part2

Gabriel Sarazin (CEA) abstract slides

Delphine Sinoquet (IFPEN) & Sébastien Le Digabel (Polytechnique Montréal) abstract slides


Abstracts

Nathalie Bartoli (ONERA)

Title: Bayesian optimization to solve black box problem with hidden constraints
Abstract: This work focuses on developing innovative methodologies for optimizing computationally expensive and complex systems, such as those found in aeronautical engineering. The proposed surrogate-based optimization, commonly known as Bayesian Optimization, leverages adaptive sampling to efficiently balance exploration and exploitation. Our in-house implementation, SEGOMOE, is designed to handle a large number of design variables—whether continuous, discrete, categorical, or hierarchical. SEGOMOE also relies on the use of a mixture of experts (local surrogate models) for both objective functions and constraints. Extensions to handle hidden constraints have also been incorporated. The performance of the resulting methods has been rigorously evaluated on a benchmark of analytical problems, as well as in realistic aeronautical applications.


Mickaël Binois (INRIA)

Title: Options for high-dimensional Bayesian optimization
Abstract: Bayesian optimization (BO) aims at efficiently optimizing expensive black-box functions, such as hyperparameter tuning problems in machine learning. Scaling up BO to many variables relies on structural assumptions about the underlying black-box, to alleviate the curse of dimensionality. To this end, in this talk we review several options for Gaussian process modeling, with emphasis on the additive and low effective dimensionality hypothesis. We discuss several practical issues related to selecting a suitable search space and to the acquisition function optimization.


François-Xavier Briol (University College London)

Title: Robust and Conjugate Gaussian Process Regression
Abstract: To enable closed form conditioning, a common assumption in Gaussian process (GP) regression is independent and identically distributed Gaussian observation noise. This strong and simplistic assumption is often violated in practice, which leads to unreliable inferences and uncertainty quantification. Unfortunately, existing methods for robustifying GPs break closed-form conditioning, which makes them less attractive to practitioners and significantly more computationally expensive. In this work, we demonstrate how to perform provably robust and conjugate Gaussian process (RCGP) regression at virtually no additional cost using generalised Bayesian inference. RCGP is particularly versatile as it enables exact conjugate closed form updates in all settings where standard GPs admit them. To demonstrate its strong empirical performance, we deploy RCGP for problems ranging from Bayesian optimisation to sparse variational Gaussian processes.


Wenlin Chen (University of Cambridge)

Title: Meta-learning Adaptive Deep Kernel Gaussian Processes for Molecular Property Prediction
Abstract: We propose Adaptive Deep Kernel Fitting with Implicit Function Theorem (ADKF-IFT), a novel framework for learning deep kernel Gaussian processes (GPs) by interpolating between meta-learning and conventional deep kernel learning. Our approach employs a bilevel optimization objective where we meta-learn generally useful feature representations across tasks, in the sense that task-specific GP models estimated on top of such features achieve the lowest possible predictive loss on average. We solve the resulting nested optimization problem using the implicit function theorem (IFT). We show that our ADKF-IFT framework contains previously proposed Deep Kernel Learning (DKL) and Deep Kernel Transfer (DKT) as special cases. Although ADKF-IFT is a completely general method, we argue that it is especially well-suited for drug discovery problems and demonstrate that it significantly outperforms previous state-of-the-art methods on a variety of real-world few-shot molecular property prediction tasks and out-of-domain molecular property prediction and optimization tasks.

Joint work with: José Miguel Hernandez Lobato (University of Cambridge)


Romain Aït Abdelmalek-Lomenech (L2S, CentraleSupélec)

Title: Active Learning of (small) Quantile Sets
Abstract: Given an expensive-to-evaluate black-box function, one is often interested in retrieving the set of inputs leading to outputs with given properties within a parcimonious number of function evaluations. In this work, we consider a multivariate function with both deterministic and uncertain inputs and focus on the estimation of a "quantile set": a set of deterministic inputs leading to outputs whose probability of belonging to a critical region is bounded by a given threshold.
Previous work (R. Ait Abdelmalek-Lomenech et al., Bayesian sequential design of computer experiments for quantile set inversion, to appear in Technometrics) gave satisfying results in this task, but proved to be insufficient for the estimation of sets whose size is small relatively to the whole domain of deterministic inputs. To tackle this issue, we propose a Gaussian processes-based sequential acquisition strategy in the joint space of deterministic and uncertain inputs. The provided strategy, coupled with a sequential Monte Carlo framework, allows to retrieve small quantile sets.

Joint work with: Julien Bect (L2S, CentraleSupélec) & Emmanuel Vazquez (L2S, CentraleSupélec)


Raphaël Carpintero Perez (Safran, CMAP Ecole Polytechnique)

Title: Learning signals defined on graphs with optimal transport and Gaussian process regression
Abstract: Machine learning algorithms applied to graph data have garnered significant attention in fields such as biochemistry, social recommendation systems, and very recently, learning physics-based simulations. Kernel methods, and more specifically Gaussian process regression, are particularly appreciated since they are powerful when the sample size is small, and when uncertainty quantification is needed. In this work, we introduce the Sliced Wasserstein Weisfeiler-Lehman (SWWL) graph kernel which handles graphs with continuous node attributes. We combine continuous Wesifeiler Lehman iterations and an optimal transport between empirical probability distributions with the sliced Wasserstein distance in order to define a positive definite kernel function with low computational complexity. These two properties make it possible to consider graphs with a large number of nodes, which was previously a tricky task. The efficiency of the SWWL kernel is illustrated on graph regression in computational fluid dynamics and solid mechanics, where the input graphs are made up of tens of thousands of nodes. Another part of the work concerns the extension of the previous approach to the case of vector outputs defined on the graph nodes (whose dimension therefore varies as a function of the number of vertices). We propose an approach based on regularized optimal transport, the aim of which is to transfer the output fields (signals) to a reference measure and then perform a reduction dimension on it.

Joint work with: Sébastien Da Veiga (ENSAI, formerly SAFRAN), Brian Staber (SAFRAN), Josselin Garnier (CMAP, Ecole polytechnique)


Vincent Chabridon (EDF)

Title: Application of HSIC-ANOVA indices to an industrial thermal-hydraulic case
Abstract: In the field of uncertainty quantification and design of computer experiments, Sobol' indices are nowadays a kind of "gold standard" tool in global sensitivity analysis (GSA). Such a fame is mainly due to their ability to partition the output variance among the inputs (assumed to be mutually independent) in a very effective and interpretable way. Based on the so-called functional "Analysis of Variance" (ANOVA) decomposition, they are able to measure the direct and indirect contribution of each input through the first-order and total-order indices. In recent years, another class of indices based on the so-called "Hilbert-Schmidt Independence Criterion" (HSIC) has gained much more attention in the GSA community, mainly due to its ability to measure input-output influence through a powerful mathematical framework that allows to go beyond variance-based effects. Coupled with powerful estimators for given data, they represent an interesting complementary tool to the Sobol' indices. However, their formulation was not based on an ANOVA-like decomposition. Recent work by Da Veiga (2021), followed by Sarazin et al. (2023), provided a clear and powerful framework for building such a decomposition, leading to the "HSIC-ANOVA" indices.
In this talk, far from being theoretical, the idea is to investigate the practical estimation of these indices in the context of a complex industrial use case involving a single Monte Carlo dataset. Some numerical insights will be provided and both advantages and limitations of these new indices will be discussed from an applied perspective.

Joint work with: Sébastien Da Veiga (ENSAI, formerly SAFRAN), Gabriel Sarazin and Amandine Marrel (CEA)


Sébastien Le Digabel (Polytechnique Montréal) and Merlin Keller (EDF)

Title: Wind farm optimization with NOMAD
Abstract: This presentation deals with the optimization of the layout of wind turbines in a wind farm, a blackbox optimization problem solved with the Mesh Adaptive Direct Search (MADS) algorithm and the NOMAD software, developed for derivative-free optimization. The objective function, representing annual energy production (AEP), is computed with the PyWake code, making it impossible to use derivatives to guide the optimization. The approach aims to maximize AEP, taking into account geographical constraints, the wake effect between wind turbines and installation costs. In addition to optimizing the layout of wind turbines, this project paves the way for the dissemination of realistic blackboxes, enriching the library of problems for derivative-free optimization and enabling rigorous benchmarking of optimization methods.


Rodolphe Le Riche (CNRS LIMOS) and Julien Pelamatti (EDF)

Title: Optimizing and metamodeling functions defined over clouds of points
Abstract: This presentation explores innovative methods for the optimization and metamodeling of complex functions defined over sets of vectors (or "clouds of points"), with various applications such as wind-farm layout or experimental design optimization. Unlike more common functions defined over vectors, functions defined over sets vectors have the specificity of being invariant with respect to the vectors permutations. Additionally, the size of the sets varies. Finally, in this work, the functions at hand are considered as "black-boxes", meaning that no information regarding their regularity and derivates is known.
The first part of this work addresses the optimization of such functions using evolutionary algorithms, focusing on stochastic perturbation operators, such as crossovers and mutations, which are developed using the Wasserstein metric. By representing sets of points as discrete measures, we leverage the Wasserstein barycenter for designing these evolutionary operators. This approach enables a precise representation of the functions’ geometric information, balancing contraction and expansion effects to enhance optimization.
In order to handle cases in which the functions are computationally costly, the metamodeling of functions defined over sets of points is also studied, with a focus on Gaussian processes. We employ substitution kernels based on Euclidean, sliced-Wasserstein, and Maximum Mean Discrepancy (MMD) distances to model complex inter-point relationships, with MMD kernels yielding particularly promising results in wind-farm simulations by adapting to the predominant wind direction.
The presentation concludes by discussing cases where the vectors belong to a non-convex domain. We also briefly show how all this work can come together to carry out Bayesian optimization over sets of vectors.

PhD work of Babacar Sow (EMSE) in collaboration with: Merlin Keller (EDF) and Sanaa Zannane (EDF)


Amandine Marrel (CEA) & Bertrand Iooss (EDF)

Title: A new estimation algorithm for more reliable prediction in Gaussian process regression
Abstract: In the context of emulating CPU-intensive numerical simulators with Gaussian Process (GP) regression, we investigated a novel algorithm for the estimation of GP covariance parameters, referred to as GP hyperparameters. The objective is twofold: to ensure a GP as predictive as possible w.r.t. to the output of interest, but also with reliable prediction intervals, i.e. representative of GP prediction error. To achieve this, we propose and extensively benchmark a new constrained multi-objective algorithm for the hyperparameter estimation. It jointly maximizes the likelihood of the observations as well as the empirical coverage function of GP prediction intervals, under the constraint of not degrading the GP predictivity.


Morgane Menz & Miguel Munoz Zuniga (IFPEN)

Title: Estimation of simulation failure set with active learning based on Gaussian Process classifiers and random set theory
Abstract: Numerical simulator crashes is a well known problem in uncertainty quantification and black-box optimization. These failures correspond to a hidden constraint and might be as costly as a feasible simulation. Hence, we seek to learn the feasible set of inputs in order to target areas without simulation failure. To this end, we will present a Gaussian Process classifiers active learning method based on the Stepwise Uncertainty Reduction paradigm. A strategy to address metamodeling objectives in the presence of hidden constraints based on the previous enrichment criterion is also proposed. The performances of the proposed strategies on an industrial case, concerning the simulation-based estimation of the accumulated damage of a wind turbine subject to several wind loads, will be presented.

Joint work with: Delphine Sinoquet (IFPEN)


Gabriel Sarazin (CEA)

Title: Towards more interpretable kernel-based sensitivity analysis
Abstract: When working with a computationally-expensive simulation code involving a large number of uncertain physical parameters, it is often advisable to perform a preliminary sensitivity analysis in order to identify which input variables will really be useful for surrogate modelling. On paper, the total-order Sobol' indices fulfill this role perfectly, since they are able to detect any type of input-output dependence, while being interpretable as simple percentages of the output variance. However, in many situations, their accurate estimation remains a thorny issue, despite remarkable progress in that direction over the past few years. In this context where inference is strongly constrained, kernel methods have emerged as an excellent alternative, notably through the Hilbert-Schmidt independence criterion (HSIC). Although they offer undeniable advantages over Sobol' indices, HSIC indices are much harder to understand, and this lack of interpretability is a major obstacle to their wider dissemination. In order to marry the advantages of Sobol' and HSIC indices, an ANOVA-like decomposition allows to define HSIC-ANOVA indices at all orders, just as would be done for Sobol' indices. This recent contribution is the starting point of this presentation.
The main objective of this talk is to provide deeper insights into the HSIC-ANOVA framework. One major difference with the basic HSIC framework lies in the use of specific input kernels (like Sobolev kernels). First, a dive into the universe of cross-covariance operators will allow to better understand how sensitivity is measured by HSIC-ANOVA indices, and what type of input-output dependence is captured by each term of the HSIC-ANOVA decomposition. Then, a brief study of Sobolev kernels, focusing more particularly on their feature maps, will reveal what kind of simulators are likely to elicit HSIC-ANOVA interactions. It will also be demonstrated that Sobolev kernels are characteristic, which ensures that HSIC-ANOVA indices can be used to test input-output independence. Finally, a test procedure will be proposed for the total-order HSIC-ANOVA index, and it will be shown (numerically) that the resulting test of independence is at least as powerful as the standard test (based on two Gaussian kernels).

Joint work with: Amandine Marrel (CEA), Sébastien Da Veiga (ENSAI, formerly SAFRAN), Vincent Chabridon (EDF)


Delphine Sinoquet (IFPEN) & Sébastien Le Digabel (Polytechnique Montréal)

Title: Optimizing with hidden constraints
Abstract: Real industrial studies often give rise to optimization problems involving complex, time-consuming simulators, which can produce failures or instabilities for certain sets of inputs: for example, problems of convergence of the numerical scheme of partial differential equations. The set of inputs corresponding to failures is often not known a priori and corresponds to a hidden constraint, also known as a crash constraint. Since observing a simulation failure can be as costly as a feasible simulation, we aim to learn the feasible region to guide the optimization process in areas without simulation failure. Therefore, we propose to couple various derivative-free optimization methods with the active learning method of the classifier presented by Morgane Menz to learn the crash domain. Different strategies for taking the hidden constraint into account in optimization will be presented and applied to a few toy problems and to an application for the calibration of a thermodynamic model.

Joint work with: Morgane Menz (IFPEN), Miguel Munoz-Zuniga (IFPEN), Christophe Tribes (Polytechnique Montréal)